Research
Electronic Structure and Dynamics and Density Functional Theory
We focus on the physics of condensed matter from small molecules up to solid-state crystals.
Molecular Systems, especially large and complex ones, can have fascinating properties, e.g., large non-linear optical coefficients, and are of interest for applications in molecular electronics and light harvesting. It is our aim to quantitatively predict the interaction of molecular assemblies with radiation and understand the interplay between molecular structure and linear and nonlinear optical properties. We are particularly interested in understanding and predicting processes of energy transfer and charge transfer. Elucidating the relation between theoretical concepts such as eigenvalues and molecular orbitals on the one hand, and experimental observables such as ionization potentials and (angular resolved) photoemission intensities on the other hand, is a particular focus of our work. Our long-term goal is the first-principles description of the complete system of nuclei, electrons and external fields, motivated by the hope that this will allow for decisive steps forward in the understanding of both natural and man-made light harvesting systems and molecular electronic devices.
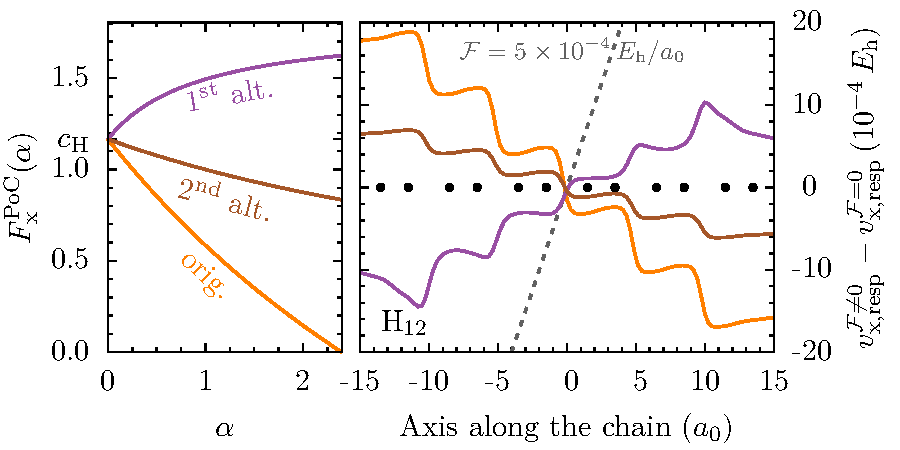
The central theorem of Density Functional Theory states that the ground-state density suffices to determine, in principle exactly, all properties of a many body system. Thus, the computationally extremely expensive calculation of the correlated many-particle wavefunction becomes superfluous. In practice, the accuracy and predictive power of density-functional calculations depend crucially on the approximations that are made for the exchange-correlation functional. Developing improved approximations for this functional by explicitly using the orbitals ("orbital functionals"), is a major aspect of our research. In particular we are interested in improving not only ground-state calculations, but time-dependent density functional theory with the aim to achieve an accurate description of charge transfer and charge transport, and of strong, non-perturbative excitations as triggered, e.g., by the fields, of powerful lasers.
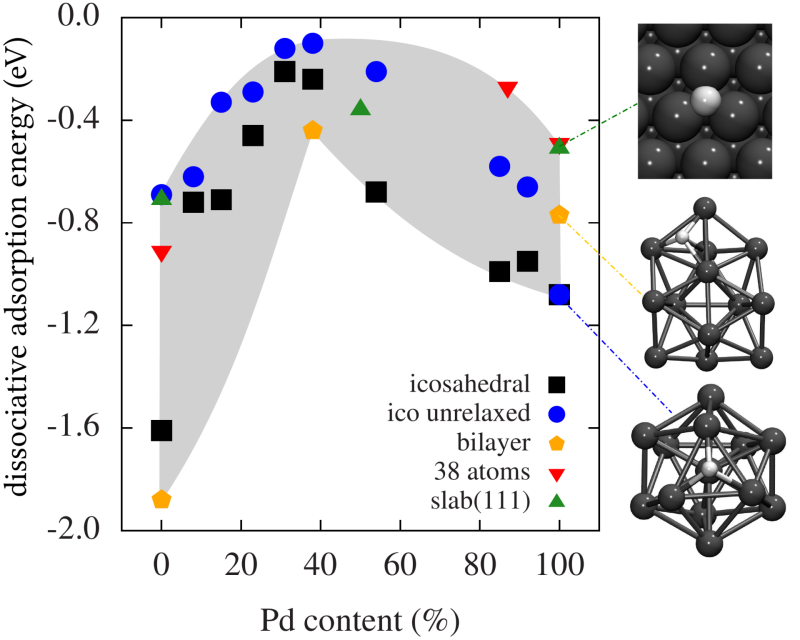
In condensed matter physics, Clusters are the link between atomic- and molecular physics on the one hand, and traditional (bulk) solid state physics on the other. A cluster consists of just a few or up to many thousands of atoms. Due to their finite size, clusters typically have properties that are very different from the ones of the corresponding bulk material. Thus, they are attractive and interesting both from a fundamental point of view (how does matter "grow" from the atom to the bulk? Which effects govern the growing? How many atoms are needed to reach the "bulk limit"?) as well as from an applied perspective (clusters are important in catalysis and are used in nanoelectronics and as building blocks for new materials).